Zadanie 1. (15pkt)
Zbiór mtcars zawiera 32 samochody (obserwacje) oraz ich parametry. Na podstawie przedstawionego wydruku oceń, czy, a jeśli tak, to która ze zmiennych wt (Weight (1000 lbs)), am (Transmission (0 = automatic, 1 = manual)) czy qsec (1/4 mile time) zostanie usunięta pierwsza z modelu liniowego mpg ~ wt + qsec + am, gdzie mpg to zużycie paliwa w milach na galon.
a) metodą selekcji wstecznej dla progu α = 0.05 (uzasadnij)
b) metodą selekcji wstecznej przy zastosowaniu kryterium Akaike (2
× log (SSE/n) + 2 × # parametrów) (uzasadnij)
c) czy model liniowy jest dobrze dopasowany? (uzasadnij)
Call:
lm(formula = mpg ~ wt + qsec + am, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.4811 -1.5555 -0.7257 1.4110 4.6610
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.6178 6.9596 1.382 0.177915
wt -3.9165 0.7112 -5.507 6.95e-06 ***
qsec 1.2259 0.2887 4.247 0.000216 ***
am 2.9358 1.4109 2.081 0.046716 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.459 on 28 degrees of freedom
Multiple R-squared: 0.8497, Adjusted R-squared: 0.8336
F-statistic: 52.75 on 3 and 28 DF, p-value: 1.21e-11
Start: AIC=61.31
mpg ~ wt + qsec + am
Df Sum of Sq RSS AIC
<none> 169.29 61.307
- am 1 26.178 195.46 63.908
- qsec 1 109.034 278.32 75.217
- wt 1 183.347 352.63 82.790
Zadanie 2 (15pkt)
Wyniki eksperymentu z podwójnie ślepą próbą, polegającego na tym, że próbka studentów z college’u (mężczyzn) uderza palcami w szybkim tempie. Próbkę podzielono losowo na dwie grupy po dziesięciu studentów każda. Każdy student wypił równowartość około dwóch filiżanek kawy, która zawierała około 200 mg kofeiny dla studentów w jednej grupie, ale była to kawa bezkofeinowa dla drugiej grupy. Po upływie dwóch godzin każdy student został przetestowany, aby zmierzyć częstotliwość stukania palca (uderzenia na minutę). Celem eksperymentu było ustalenie, czy kofeina powoduje wzrost średniej częstości uderzania palcami. Na poniższym wykresie przedstawiono wyniki:
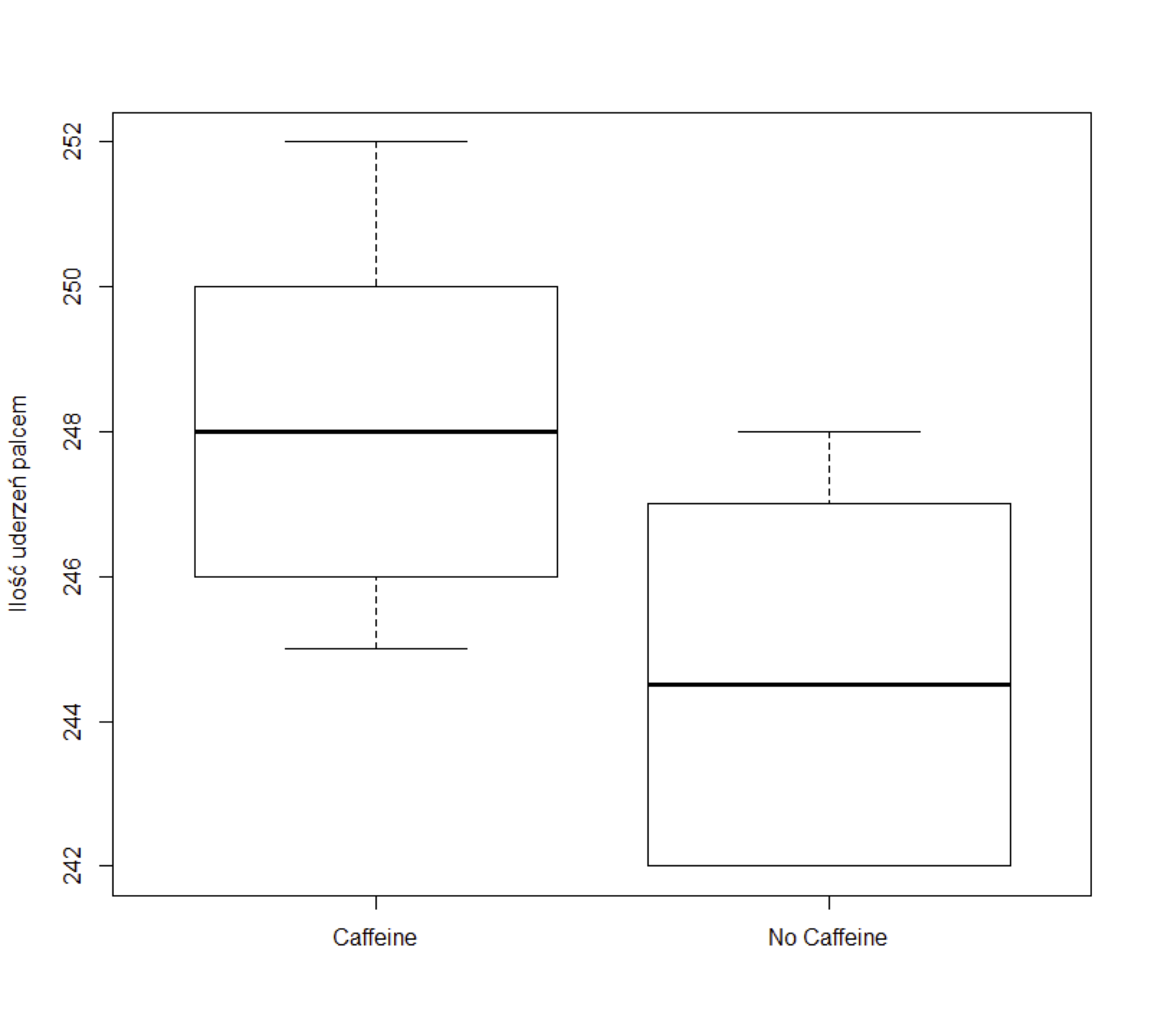
a) czy na podstawie powyższego wykresu możemy stwierdzić, że istnieje statystycznie istotna różnica pomiędzy grupami (odpowiedź uzasadnij).
b) czy na podstawie poniższych wyników testu statystycznego możemy stwierdzić, że istnieje statystycznie istotna różnica pomiędzy grupami (odpowiedź uzasadnij).
> t.test(Taps ~ Group, data= CaffeineTaps, paired=FALSE)
Welch Two Sample t-test
data: Taps by Group
t = 3.3942, df = 17.89, p-value = 0.003255
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.332616 5.667384
sample estimates:
mean in group Caffeine
248.3
mean in group No Caffeine
244.8
c) Jaka jest hipoteza zerowa a jaka alternatywna dla powyższego testu?
Zadanie 3 (20pkt)
Reguły decyzyjne są jednym z narzędzi reprezentacji wiedzy (modelowania danych). Opisują one związki między atrybutami warunkowymi (zwykle wieloma), a atrybutem decyzyjnym, za pomocą implikacji: po lewej stronie znajdują się warunki wyrażone pewną formułą logiczną, po prawej – wartość atrybutu decyzyjnego.
a) W jaki sposób odbywa się klasyfikacja za pomocą reguł? Czy wszystkie przypadki ze zbioru testowego na pewno zostaną sklasyfikowane?
b) Jakie są parametry reguł? Co to jest wsparcie (support) a co to jest dokładność (accuracy) reguły?
c) Czy da się wydobyć reguły decyzyjne z drzewa decyzyjnego? Jeśli tak to w jaki sposób?
d) Co to są reguły asocjacyjne i do czego służą? Czym różną się reguły asocjacyjne od reguł decyzyjnych? Co je łączy?
Zadanie 4 (25pkt)
Przeprowadzono analizę zbioru IRIS, który zawiera 4 cechy irysów, które pochodzą z 3 gatunków irysów: setosa, versicolor, and virginica. W bazie mamy opisane po 50 sztuk z każdego gatunku, co daje nam 150 obserwacji.
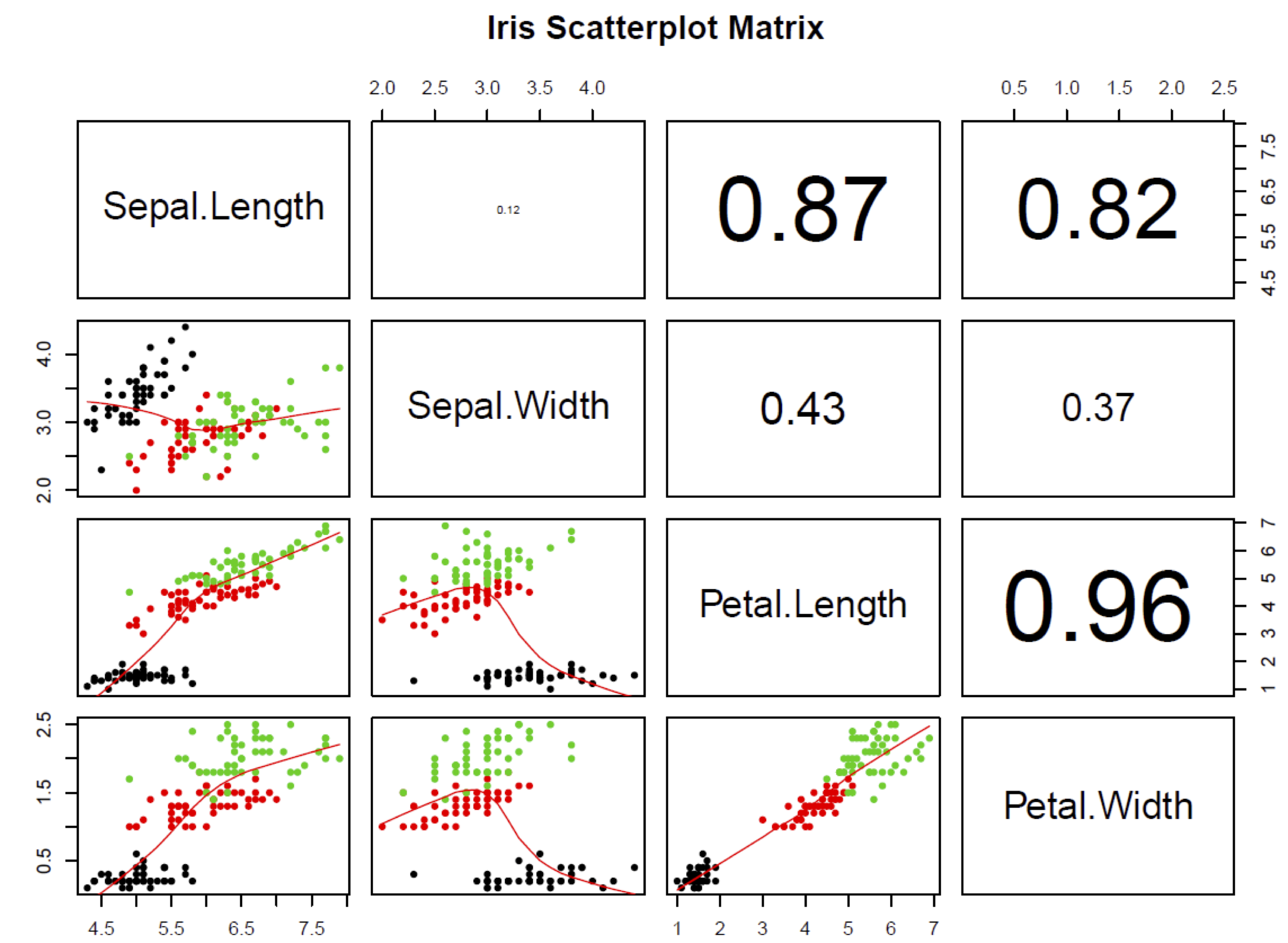
a) na podstawie macierzy korelacji „Iris Scatterplot Matrix” określ, które zmienne są ze sobą silnie skorelowane.
b) jakie problemy podczas budowania modeli, zwłaszcza liniowych, powoduje silne skorelowanie zmiennych?
c) czy trzy klasy irysów są liniowo separowane? (uzasadnij)
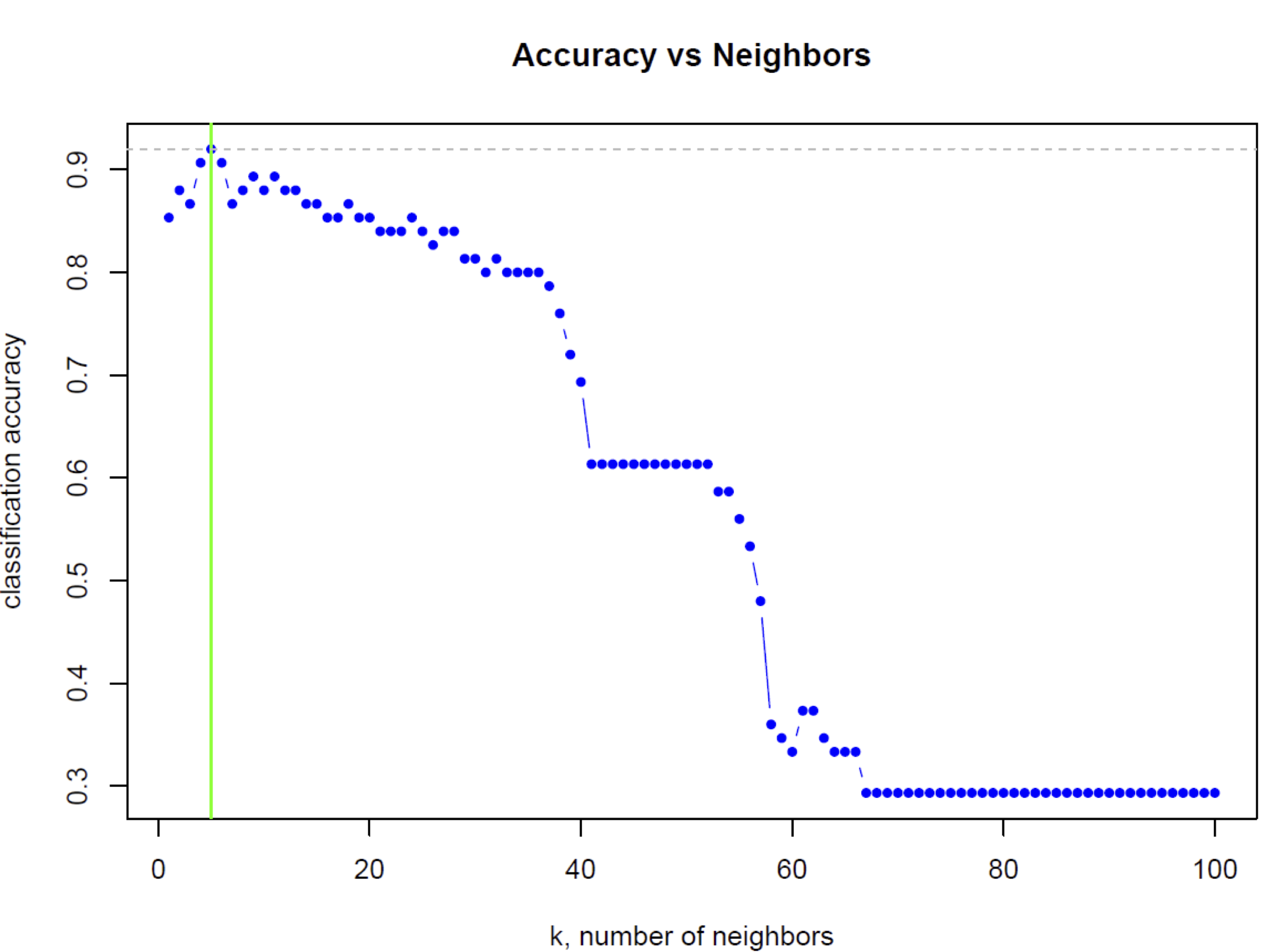
d) Dla zbioru danych IRIS zbudowano kilka klasyfikatorów KNN dla rożnych k oraz zmierzono ich dokładność klasyfikcji (classification accuracy). Wykres „Accuracy vs Neighbors” prezentuje testowanie algorytmu KNN dla k od 1 do 100 co 1. Jakie jest optymalne k? (uzasadnij)
e) Dlaczego dokładność klasyfikacji powyżej k=67 jest taka niska (mniejsza niż 0.3)? (uzasadnij)
Zadanie 5. (20pkt)
Klastrowanie jest techniką grupowania podobnych instancji w klastry zgodnie z pewną miarą odległości. Główną ideą jest umieszczenie obserwacji, które są podobne (to znaczy blisko siebie) do tego samego klastra, przy jednoczesnym zachowaniu odmiennych punktów (to znaczy tych dalej od siebie od siebie) w różnych klastrach.
a) Algorytmy grupowania są oparte na dwóch zasadniczo różnych podejściach. Co to są za podejścia? Czym się różną? (uzasadnij)
b) Algorytm k-średnich jest prawdopodobnie najczęściej stosowaną metodą klastrowania. Czym jest parametr k? Jak wyznaczyć parametr k? Co to jest reguła „łokcia”
c) Wymień wady i zalety algorytmu k-średnich (po 2)
d) Miara odległości w algorytmach klasteryzacji jest bardzo ważna. Co to są odległości euklidesowa a co to są odległości nie-euklidesowe? Wymień najbardziej znane miary odległości dla każdej z grup (po 2).

